
上一篇文章我们的数据来源属于年度数据,得到回归结果并不显著,但相关性极强。接下来本篇章将结合回归分析模型,从月度数据的角度对粗钢月度产量实现100、200、500万吨压减目标下,预估线盘月度产量变化情况。注意:100、200、500万吨是由年度粗钢产量压减1000、2000、5000万吨粗略除以10计算得出,同时因为数据本身具有波动性和季节性,叠加粗钢减产情况下分品种不一定同比例下降影响下,线盘产量影响情况主要呈现为粗钢与线盘产量间统计关系得出,可能与现实存在部分出入,理性决策需结合现实情况加以斟酌判断。
本文进行回归分析模型采用excel工具,其中线盘产量数据来源采用Mysteel调研线材钢铁企业实际产量周度数据月度合计值变频值,粗钢产量数据来源选择统计局公布月度日均产量数据乘以月度天数。
首先,我们对粗钢-线盘数据做散点图,选用多项式趋势线进行拟合,拟合公式为y = -1E-05x2 + 0.2279x - 473.34,同时得到R2 = 0.2255,表示粗钢-线盘产量数据之间存在一定正相关性,但相关性并不强。
这里补充一下,R Square是测定系数,也叫拟合优度,是相关系数R的平方,同时也等于表2中回归分析SS/(回归分析SS+残差SS),这个值在0~1之间,越大,代表回归模型与实际数据的拟合程度越高。当这个值大于0.8时表示强正相关。

结合上图可知,趋势线拟合分析呈现相关性,但相关性强度偏弱。接下来进行回归预测分析。我们在95%置信区间下计算得到的回归分析模型处理结果如下。

相关性的显著程度我们主要依据Multiple R、F检验和P值结果来进行判断,其中Multiple R=0.46,佐证了相关性不强的结论;但P值=0.0085<=0.01,表明结果具有极其显著的统计学意义。我们得出的回归方程为y=217.79+0.05x。
这里补充一下,其中Multiple R是指相关系数R,值在-1与1之间,越接近-1,代表越高的负相关,反之,代表越高的正相关关系;F检验主要是检验因变量与自变量之间的线性关系是否显著,用线性模型来描述他们之间的关系是否恰当,越小越显著;如果P值>0.05, 则结果不具有显著的统计学意义,如果0.01

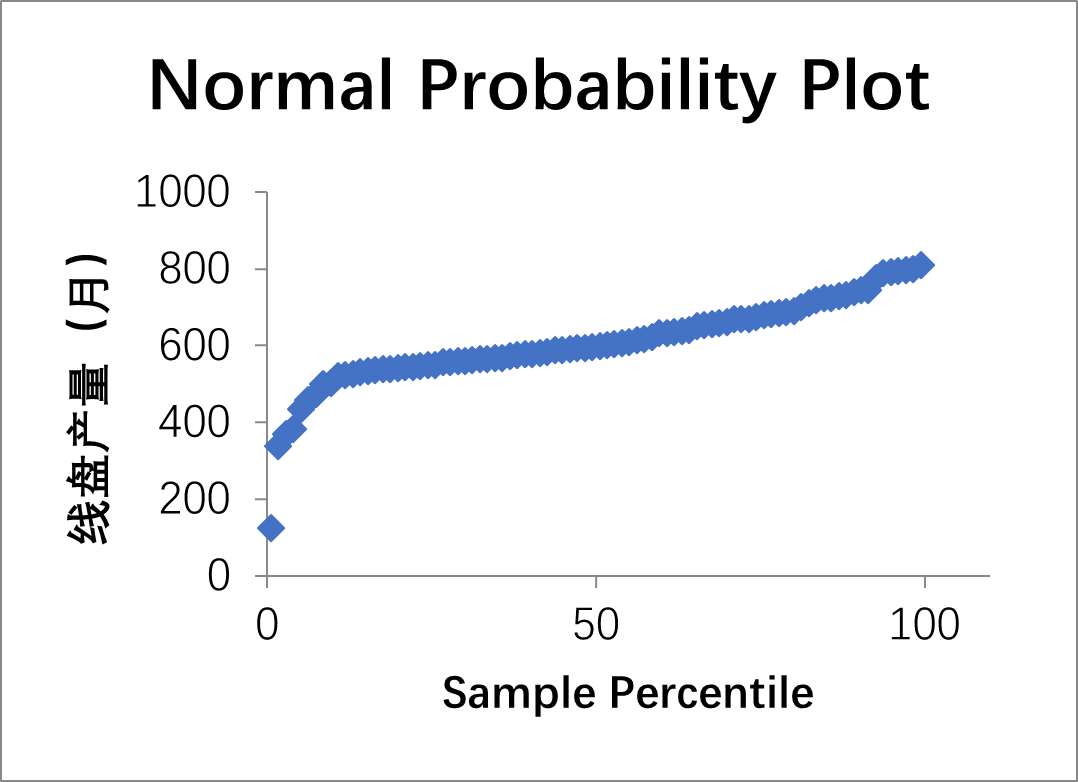

最后,我们根据回归方程y=217.79+0.05x进行计算粗钢压减100、200和500万吨情况下线盘产量影响值。根据计算得出,在粗钢产量压减100万吨情况下,线盘产量减少134.33万吨;在粗钢产量压减200万吨情况下,线盘产量减少129.33万吨;在粗钢产量压减500万吨情况下,线盘产量减少114.33万吨。
注意:本篇涉及产量均为月度合计产量。
系列文章汇总如下:
Mysteel:粗钢压减背景下的线盘产量影响(一)基础知识篇
https://gc.mysteel.com/22/0629/17/E4832892A9CBBC60.html
Mysteel:粗钢压减背景下的线盘产量影响(二)回归分析年度数据篇
https://gc.mysteel.com/22/0630/13/0BB0CF518AC4FEC3.html
Mysteel:粗钢压减背景下的线盘产量影响(三)回归分析月度数据篇
https://gc.mysteel.com/22/0630/13/E8C4257D3A56B092.html